hashTable 哈希表又叫散列表是一种键值对存储结构的一种数据结构,python的字典就采用这种数据结构,其效率在理想状态下是O(1),但是在最差的情况下是O(n),这儿我们按照思路自己实现一个,其基本实现过程为
申请一个定长m的列表作为存储空间,在每个位置上设置值为None,列表根据索引取值/设置的时间复杂度是O(1)
列表上每个位置在有值的情况下,其数据结构为一个[key,value]的列表
对设置的key进行hash求值后得到值p,再对p和m求模的到值n,这个值n就是该键值对存储在列表中的位置
当被作为存储的列表的空间被占用到一定比例的时候进行扩容
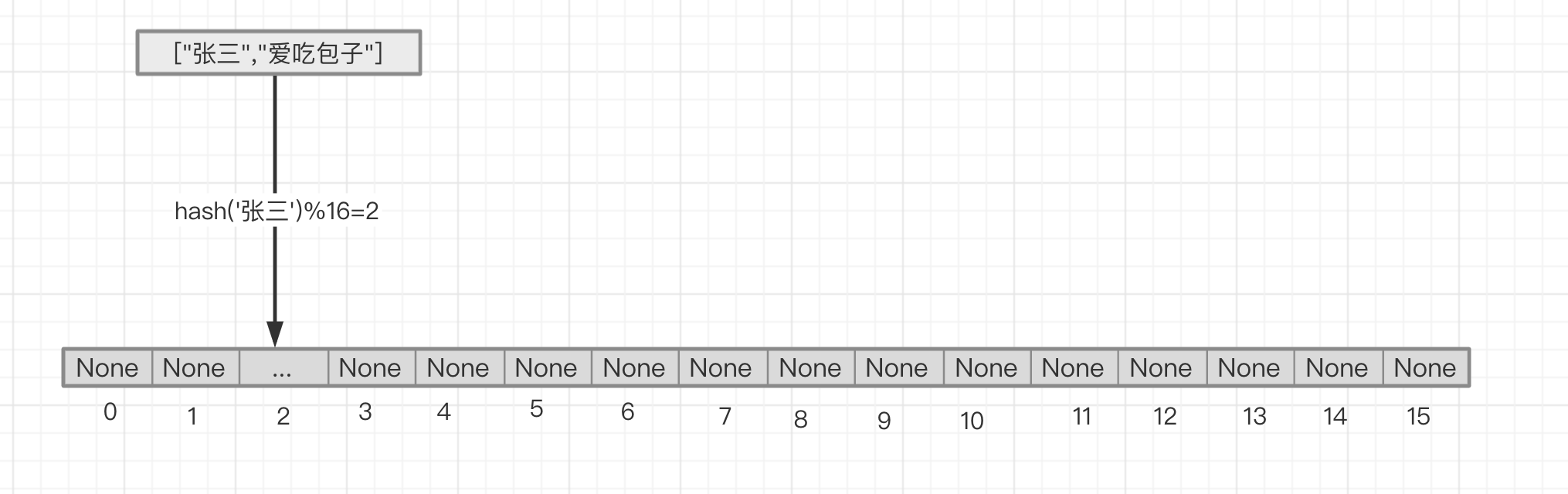
k-v为 '张三'对应'爱吃包子',对张三求hash之后再与列表长度16进行求模,得到值2,即'张三'对应'爱吃包子'这个键值对就应该存储的list的2这个index位置上。取值时,进行同样的操作即可。
但是当然上述情况可能会出现哈希冲突,即不同的key最后得到的n值是一样的,好巧不巧,罗老师爱馒头,而罗老师这个key算出在列表中的位置也是2,这可怎么办呢?
开放寻值法或者链接法来进行冲突解决。
开放寻值 开放寻值是指当张三占据了2号位的时候,罗老师也想进到2号位来,这个时候后来的罗老师只能屈居后位来,在2号位之后找一个位置填进去,至于怎么找后一位,有线性探测、二次探测、双重散列等方式。这儿我们使用最简单的线性探测。
在查找罗老师的时候,先通过hash('罗老师')%16=2求出罗老师在2号位,如果2号位存的值的key不是罗老师,那我们就去找3号位,如果3号位也不是罗老师,那我们就找4号位,以此类推直到找到罗老师,值得注意得是,在删除一个key时,同时也要将被删除值的右边的所有元素直到第一个None值重新散列。
代码实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 class HashTable (object 0.75 def __init__ (self, size ):0 None for _ in range (size)]def _get_index (self, key ):return hash (key) % self.sizedef _loop_index (self, index ):for _ in range (self.size - 1 ):if index > self.size - 1 :0 yield index1 def get (self, key ):for index in self._loop_index(self._get_index(key)):if data is not None :if data[0 ] == key:return data[1 ]else :return None return None def set (self, key, value ):if self.used_index / self.size > self._reload_factor:for index in self._loop_index(self._get_index(key)):if data is None :1 return if data[0 ] == key:return def _reload (self ):2 None for _ in range (self.size)]for i in old_container:if i is not None :set (i[0 ], i[1 ])1 def delete (self, key ):0 for index in self._loop_index(self._get_index(key)):if data is not None and data[0 ] == key:None 1 break for index in self._loop_index(del_index+1 ):if data is None :break None set (*data)1
链接法 链接法是指,当张三占据了2号位的时候,罗老师也想进到2号位来,那么这个时候我们二号位上的数据结构改变成[key,value]为元素的一个链表,把["罗老师","爱吃馒头"]作为链表上的节点的元素的节点添加到["张三","爱吃包子"]作为元素的链表的节点的后面
当需要找到罗老师的时候,根据hash('罗老师')%16=2求出罗老师在2号位, 然后遍历2号位上的链表,直到找到罗老师,当然同样存在扩容的问题,应为如果一个index上的链表过长也会导致查询时间变慢,极端情况下会出现O(n)的查询效率
下面是代码实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 class LinkedNode (object def __init__ (self,data ):None class Linked (object def __init__ (self,first_data ):def append (self,data ):if self.first_node == None :return def delete_node (self,node ):if node == self.first_node:if self.first_node == self.last_node:None else :return None while p.next_node:if p == node:return def for_each (self ):while p.next_node:yield pyield pclass HashTable (object def __init__ (self,size ):None for _ in range (size)]def _get_index (self, key ):return hash (key) % self.sizedef set (self,key,value ):if linked is None :return for i in linked.for_each():if i.data[0 ] == key:1 ] = valuereturn def get (self,key ):if linked is None :return None for i in linked.for_each():if i.data[0 ] == key:return i.data[1 ]return None def delete (self,key ):if linked is None :return if linked.first_node == None :None for i in linked.for_each():if i.data[0 ] == key:
布隆过滤器 当我们在写python代码时,如果遇到需要去重的时候,我们大家第一反应是使用set,其实set的实现和map相似,都是hash表,但是如果要进行海量数据进行去重时,比如采集系统的url去重可能上亿或者更多的url需要去重,set就需要占用大量的内存空间,如果采用链表或者树,那么时间复杂度又上去了。这时布隆过滤器就登场了。
布隆过滤器 (英语:Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难。
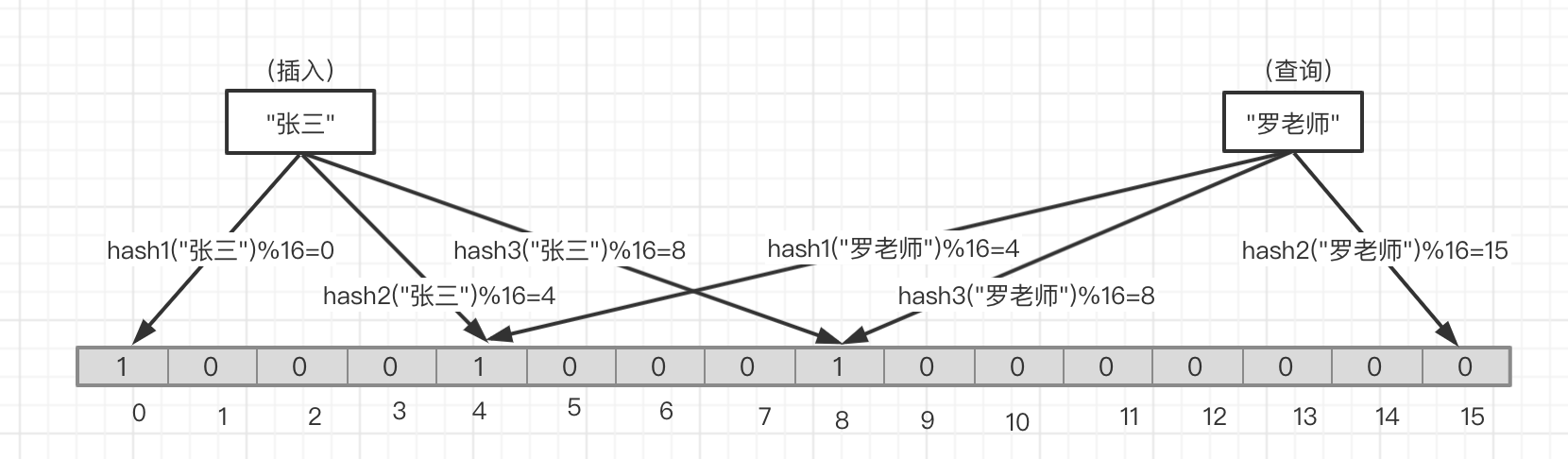
如 图五 ,当我们插入'张三'时分别通过三个hash函数和bitmap(不再是list了,虽然list也可以,但是bitmap更加合适,更节省空间)的长度进行求模(就如同上面hashTable一样)求的分别的index,然后将这些index位上的bit设置为1(无论之前的状态是0是1)
如 图五 ,当查询'罗老师'的时候,一样通过这三个hash函数求得分别的index,然后去取对应的bit的状态,如果都是1则'罗老师'是存在的,如果有任何一位不是0,就如图所示,hash2函数得到的index 15 是0,则说明'罗老师'之前没有被设置过
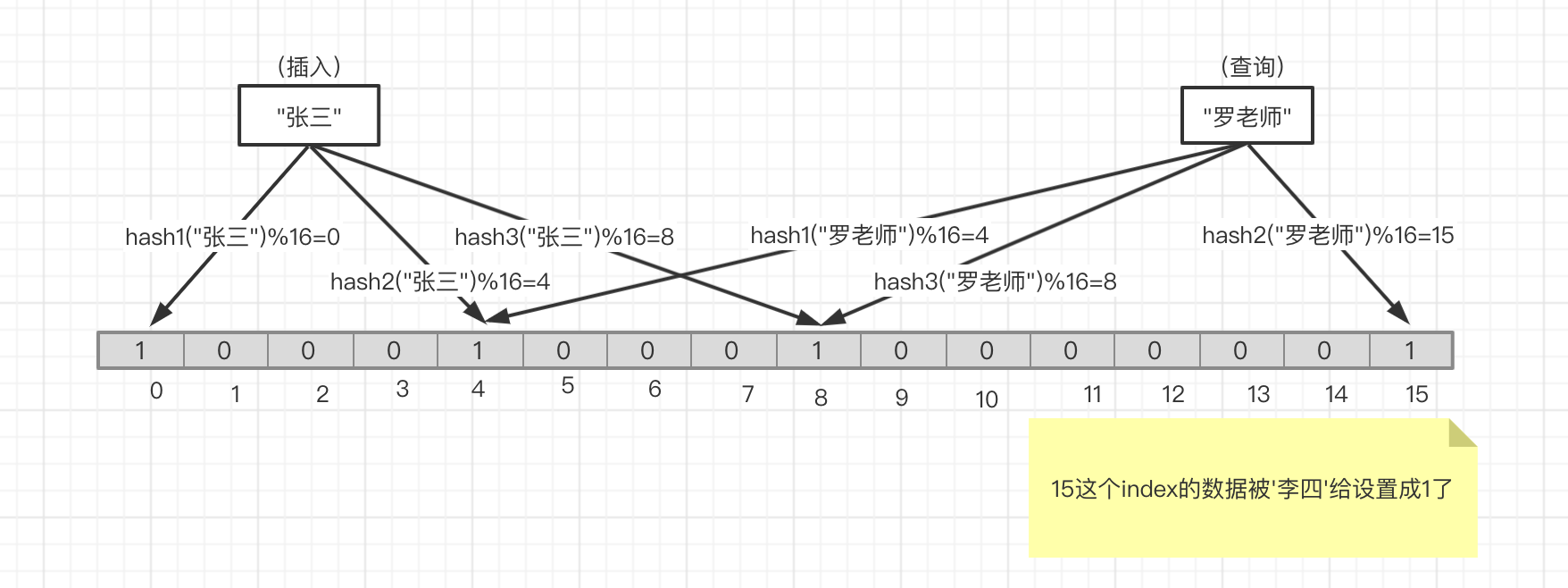
如图六 ,上述情况如果'罗老师'并没有被插入过,但是好巧不巧'李四'把15号位设置成了1,那么当我们查询'罗老师'在不在的时候就有可能出现误判,究其原因还是因为hash碰撞导致的。这也就是上面所说的存在误判的原因
不能删除的原因是因为一个bit位可能被多个key置为1过,如果将此位重置成0,那么将影响到多个key的查询。这就是上面所讲的删除困难的所在。
布隆过滤器参数的确定 如果布隆过滤器的长度太小,所有的 bit 位很快就会被用完,此时任何查询都会返回“可能存在”;如果布隆过滤器的长度太大,那么误判的概率会很小,但是内存空间浪费严重。类似的,哈希函数的个数越多,则布隆过滤器的 bit 位被占用的速度越快;哈希函数的个数越少,则误判的概率又会上升。因此,布隆过滤器的长度和哈希函数的个数需要根据业务场景来权衡。
我们假设 k 为哈希函数的个数,m 为布隆过滤器的长度,n 为插入元素的个数(需要处理的数据个数),p 为误报率,则:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 from bitarray import bitarrayimport mathimport hashlibclass BloomFilter (object def __init__ (self, item_size, misdeclaration_rate=0.001 , hash_random_code="Jsk" ):if misdeclaration_rate > 0 and misdeclaration_rate < 1 else 0.001 def _init_bits (self ):int (-self.item_size * math.log(self.misdeclaration_rate) /2 ) * math.log(2 )))f"bit size {size} " )f"it cost {round (size/8 /1024 /1024 ,3 )} M" )"0" ) @staticmethod def get_md5 (key ):return h.hexdigest()def _init_hash_func (self ):int (max (1 ,round (self.bits_size / self.item_size * math.log(2 ))))f"func size {size} " )lambda x: BloomFilter.get_md5(x + i * self.hash_random_code)for i in range (size)def _get_index (self, key ):return [int (x(key), base=16 ) % self.bits_size for x in self.hash_funcs]def set (self, key ):for i in index:True def check (self, key ):for i in index:if not self.bitmap[i]:return False return True if __name__ == "__main__" :100000000 )set ("ksu" )"ksu" ))"ksp" ))
执行上面的脚本输出:
1 2 3 4 5 bit size 1437758756
1亿个元素的去重,误报率在0.1%,只需要170M的空间就能进行,在实际的生产中,大多数情况下的会使用redis作为布隆过滤器的存储,redis的string类型有SETBIT和GETBIT命令,相关实现网上也有很多例子。
 例如设置
例如设置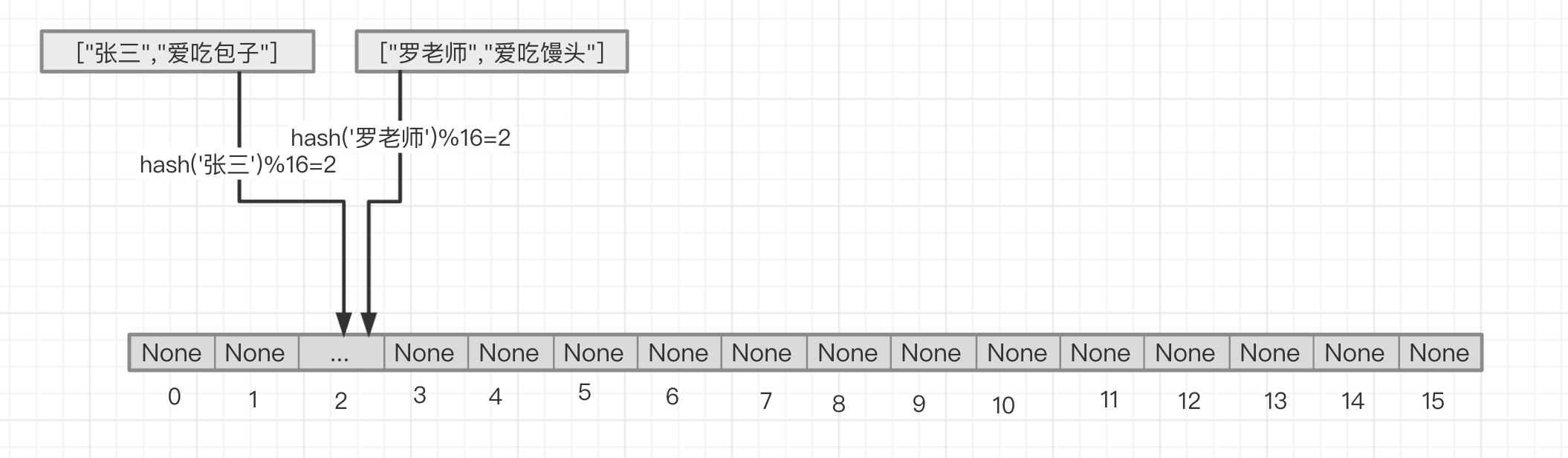 这种情况下,可以通过
这种情况下,可以通过